Tiếp cận ban đầu trong ước lượng độ đo rủi ro

http://toantaichinhblog.wordpress.com/2013/07/02/tiep-can-ban-dau-trong-uoc-luong-do-do-rui-ro/

Tiếp cận ban đầu trong ước lượng độ đo rủi ro

Bài viết sau đây sẽ là tiếp nối của chuỗi bài viết về độ đo rủi ro, chúng ta sẽ làm việc với 2 vấn đề cơ bản đó là làm rõ định nghĩa về mặt toán học của độ đo rủi rotrong đó chú trọng vào vấn đề thế nào là một độ đo rủi ro Coherent (có thể tạm dịch là độ đo rủi ro “nhất quán” hoặc “chặt chẽ”) và những giả định quen thuộc xung quanh việc ước tính VaR.

I, Khái niệm về độ đo rủi ro.

Chúng ta mô hình sự bất định của thị trường Tài chính bởi không gian xác suất . Gọi M là tập các biến ngẫu nhiên hữu hạn (hầu chắc chắn) trong không gian xác suất  nêu trên.  là một tập con của . Các nhà đầu tư tham gia thị trường tài chính thông qua việc nắm giữ các danh mục danh mục đầu tư. Rủi ro tài chính của việc nắm giữ danh mục biểu hiện bởi mức thua lỗ tiềm ẩn sau kỳ đầu tư và được mô hình hoá bởi biến ngẫu nhiên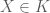 

Một độ đo rủi ra được định nghĩa là một ánh xạ từ một tập hợp các biến ngẫu nhiên tới tập các số thực .

Định nghĩa: Ánh xạ 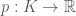 gọi là độ đo rủi ro của danh mục. Danh mục với mức thua lỗ  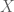có mức rủi ro ro 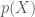. Liên hệ với thực tiễn, trong quản trị rủi ro  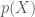có thể là một khoản dự phòng, khoản thế chấp, vốn dự trữ,…

Độ đo rủi ro giúp nhà đầu tư đo lường được mức độ rủi ro mà họ sẽ phải gánh chịu trong thời gian nắm giữ danh mục. Tuy nhiên một độ đo rủi ro như thế nào thì cung cấp cho nhà đầu tư một nguồn có cơ sở hay đáng tin cậy để thực hiện công tác quản trị rủi ro? Dưới đây chúng ta sẽ trình bày về độ đo rủi ro Coherent (độ đo rủi ro nhất quán).

 II, Độ đo rủi ro Coherent

Các độ đo rủi ro Coherent (một số tài liệu dịch là các độ đo rủi ro nhất quán hoặc các độ đo rủi ro chặt chẽ) thoả mãn các tính chất sau

a, Bất biến theo phép tịnh tiến (Translation Invariance): Với mọi  khi đó:

b, Cộng tính dưới (Subadditivity): Với mọi  khi đó:

c, Thuần nhất dương (Homogeneity): Với mọi  ta có:

d, Đơn điệu tăng (Monotonicity): Với mọi  và  (hầu chắc chắn) khi đó:

Ý nghĩa của các tính chất này được giải thích như sau:

a, Tính chất bất biến theo phép tính tiến: Với danh mục có độ đo rủi ro 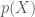 khi bổ sung tài sản phi rủi ro có giá trị  thì mức độ rủi ro của danh mục giảm còn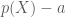 

b, Tính chất cộng tính dưới : Rủi ro của danh mục gồm nhiều yếu tố rủi ro ở đây là  sẽ nhỏ hơn hoặc bằng với tổng rủi ro của các yếu tố rủi ro thành phần. Tính chất này phù hợp với lý thuyết đa dạng hoá danh mục đầu tư (diversification), nhà đầu tư không nên bỏ trứng vào 1 rổ mà phải phân bổ vào nhiều nơi khác nhau.

c, Tính chất thuần nhất dương: Đối với những danh mục có quy mô càng lớn thì độ rủi ro càng cao.

d, Tính chất đơn điệu tăng: Danh mục có mức thua lỗ tiềm ẩn cao thì rủi ro cũng cao.

III, Một số giả định xung quanh việc ước tính VaR:

Thông thường để thiết lập một mô hình Tài chính cần có các giả định đầu vào (input factors), đối với việc tính toán VaR chúng ta cũng cần có những giả định (assumption). Chúng ta sẽ làm quen với một số giả định thông dụng trong các mô hình tính toán VaR tham số, đối với các phương pháp tiếp cận VaR phi tham số sẽ có những đặc điểm khác mà ta sẽ bàn ở các mục sau.

1, Bước ngẫu nhiên

Một biến ngẫu nhiên 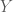 được định nghĩa là một bước ngẫu nhiên (Random walk) nếu  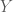được biểu diễn:

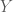Trong đó  biểu thị giá trị của  tại mốc thời gian  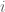và  là nhiễu trắng (có trung bình bằng 0, phương sai không đổi và hiệp phương sai bằng 0). Điều đó có nghĩa là:

Khi đó theo tính chất của kỳ vọng ta có:

Điều đó có nghĩa là quá trình ngẫu nhiên  là một Martingale. Với giả định này, chúng ta xem rằng giá trị tương lai của biến ngẫu nhiên không phụ thuộc vào giá trị trong quá khứ của chúng.

2, Tính dừng: Một chuỗi được gọi là dừng nếu kỳ vọng, phương sai và hiệp phương sai không thay đổi theo thời gian. Điều này có nghĩa là phân phối xác suất của chuỗi là không thay đổi theo thời gian. Có như vậy thì chúng ta mới thực hiện việc dự báo giá trị tương lai của biến ngẫu nhiên dựa trên phân phối xác suất của nó trong một khoảng thời gian nhất định được.

3, Giá trị tài sản không âm: Giá trị của tài sản tài chính, ví dụ như giá chứng khoản, tỷ giá,… được giả sử là không âm () tại mọi thời điểm.

4, Thời gian cố định: Với giá định này, chúng ta coi rằng điều gì đúng cho một giai đoạn thì cũng đúng cho nhiều giai đoạn khác. Ví dụ như ta xem xét sự đúng đắn trong vòng 1 tuần thì cũng có thể mở rộng thành 1 tháng, hoặc 1 năm,… Chúng ta có công thức mở rộng sau:

Trong đó 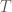 viết tắt của  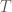ngày và  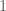có nghĩa là 1 ngày. Như vậy khoảng thời gian càng lớn thì giá trị VaR càng tăng lên.

5, Phân phối chuẩn: Phân phối chuẩn (Normal Distribution) nắm giữ 1 vai trò quan trọng trong Tài chính, đây là giả thiết không chỉ của các mô hình phân tích VaR mà còn rất nhiều mô hình khác nữa. Với giả thiết này để ước lượng VaR người ta giả sử rằng chuỗi Tỷ suất sinh lợi của Tài sản tuân theo quy luật phân phối chuẩn, ngoại trừ một số phương pháp tiếp cận VaR phi tham số như mô phỏng Monte Carlo thì giả thiết này không cần thiết. Giả thiết này giúp cho quá trình tính toán VaR trở nên đơn giản hơn thông qua định lý về phân phối chuẩn đa biến, tuy nhiên ngày nay, các chuỗi lợi suất của tài sản Tài chính không phải lúc nào cũng tuân theo phân phối chuẩn và từ đó dẫn đến những ước lượng không chính xác về VaR. Để giải quyết vấn đề về phân phối biên duyên (marginal distribution) của mô hình đa biến thì công cụ Copula trong lý thuyết xác suất-thống kê là 1 sự lựa chọn đang được áp dụng trên thế giới. Vấn đề này sẽ tiếp tục được đề cập trong phần tiếp theo.